Beamforming & Coupling: Simulating Dual Antenna Arrays on a Telecom Tower

This is the last of our 6-part tutorial series hosted by experienced antenna engineer Katerina Galitskaya who is documenting her experience learning Nullspace as a new user. Over six tutorials she progresses from simulating a single bow-tie antenna to building full arrays and exploring beamforming techniques, sharing direct comparisons to other full-wave 3D EM simulation tools.

The full video version of this tutorial is available to watch on YouTube.

Problem Statement

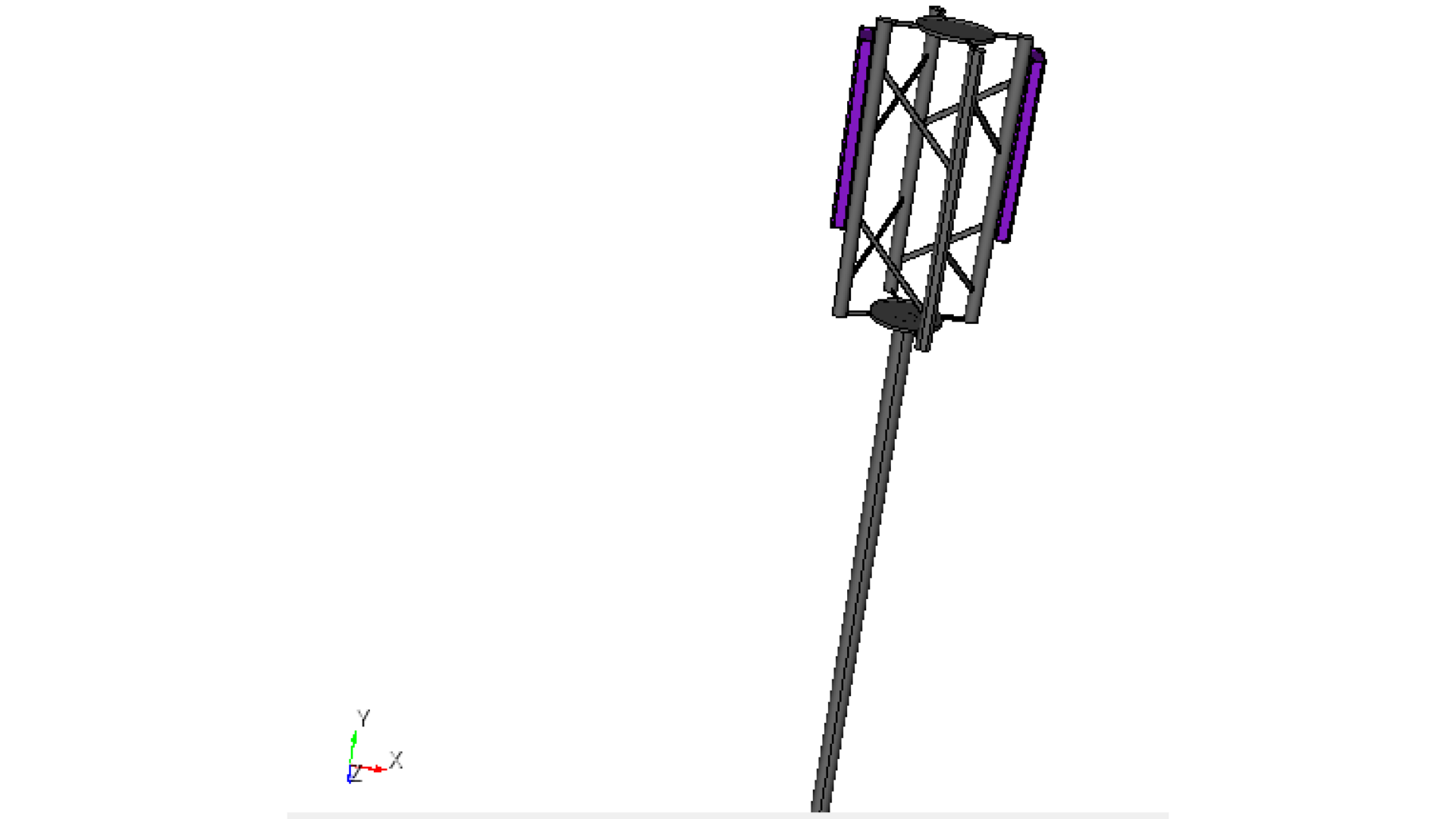
This tutorial covers the modeling, simulation, and post-processing of an electrically large problem consisting of two 4-element antenna arrays mounted on a 10-meter telecom tower. Modern cellular sites commonly host multiple antennas, making mutual coupling a critical performance consideration. The completed 3D geometry is shown in Figure 1.

Fig. 1 Two integrated antenna arrays on a tower

Model setup

Preparation: Use the installed antenna array model from the fifth tutorial.

Units: CAD model is defined in millimeters, converted to meters during simulation.

Frequency sweep: 0.5–1.5 GHz (11 points).

Radiation data: Dense far‑field grid (2-degree step in theta and phi).

Extracted metrics: S21 coupling between antennas, boresight gain, gain vs. frequency, 2D radiation cuts, and 3D radiation pattern.

CAD Model and Meshing

Begin by opening Prep and setting your working directory to a folder where you plan to complete this example.

Use the parameter definitions and modeling instructions from the previous tutorial.

#{inner_width=1.7}

#{outer_width=30}

#{leng=42}

#{port=1.7}

#{subH=0.767}

#{subW=140}

###substrate geometry

brick x {subW} y {subW} z {subH}

volume 1 rename "substrate"

move Volume substrate z {-subH/2} include_merged 

###ports geometry

create vertex {-port/2} {-port/2} 0 

#{v1 = Id("vertex")}

create vertex {port/2} {-port/2} 0

create vertex {port/2} {0} {port/4}

create vertex {-port/2} {0} {port/4}

create surface vertex {v1} to {v1+3}

#{port_pos = Id("surface")}

surface {port_pos} copy reflect y 

#{port_neg = Id("surface")}

###antenna geometry

create curve location {-outer_width/2} {port/2+leng} 0 location {outer_width/2} {port/2+leng} 0

#{c1 = Id("curve")}

create curve location {-outer_width/2} {port/2+leng} 0 location {-inner_width/2} {port/2} 0

create curve location {outer_width/2} {port/2+leng} 0 location {inner_width/2} {port/2} 0

create curve location {-inner_width/2} {port/2} 0 location {inner_width/2} {port/2} 0

create surface curve {c1} to {c1+3}

#{dipole_top = Id("surface")}

surface {dipole_top} copy reflect y nomesh 

#{dipole_bot = Id("surface")}

project surface {port_pos} {port_neg} onto surface 1 imprint

project surface {port_pos} {port_neg} {dipole_top} {dipole_bot} onto surface 2 imprint

###ground plane

create surface rectangle width 300 zplane 

#{GND = Id("surface")}

#{gnd_H=70} 

move Volume 6 z {-gnd_H} include_merged 

###4-element array creation

Volume 1 2 3 4 5 6 copy move x 0 y 170 z 0 repeat 3 group_results 

unite surface {GND} 36 53 70 

#{GND = Id("surface")}

####radome import

import step "radome.step" heal group "radome"

#{radome = Id("volume")}

move volume {radome} y -170 include_merged 

rotate Volume all angle 90 about Y include_merged preview 

rotate Volume all angle 90 about Y include_merged 

###tower import

import step "TelecomMast_simplified.step" heal group "Tower" 

#{tower = Id("volume")}

move volume {tower} x -580 y -11000 z 130 include_merged 

### Remove small features and surfaces from tower model

remove surface 181, 200 connected_sets

remove surface 88, 170, 199 connected_sets

select surface 183 include similar

remove surface 179, 183 connected_sets

select surface 198 118 203 include similar

remove surface 118, 198, 203, 204 connected_sets

remove surface 168

remove surface 182, 201 connected_sets

remove surface 154, 202 connected_sets

remove surface 180

remove surface 184

select surface 143 207 include similar

remove surface 143, 151, 206, 207 connected_sets

remove surface 187

remove surface 91, 92, 126 connected_sets

remove surface 122, 150, 158 connected_sets

remove surface 99, 134, 167 connected_sets

webcut volume 26 with sheet extended from surface 146 

webcut volume 27 with sheet extended from surface 205 

delete volume 27

remove surface 123, 127, 128 connected_sets

Copy and position the first array to the opposite pole. 

Volume 1 2 3 4 5 6 7 8 9 10 11 13 14 15 16 17 19 20 21 22 23 25 copy 

group 'second_array' add Volume 29 35 40 45 50 30 31 32 33 34 35 36 37 38 39 41 42 43 44 46 47 48 49

group second_array rotate 180 about Y include_merged

second_array move x -1160 y 0 z 250

imprint all

merge all

Materials & Voltage Sources

Use the material.py script to define the material library. Besides PEC, this model uses FR-4 and glass fiber. Open the Nullspace EM environment and load the material.py file before assigning materials.

from nsem import *

ml=MaterialLibrary()

ml.add_material(Material('FR-4', 'green', MaterialProperty('constant',real=4.4, losstan=0.02), MaterialProperty('constant',real=1.0, imag=0.0)))

ml.add_material(Material('glassfiber', 'grey', MaterialProperty('constant',real=4.7, losstan=0.09), MaterialProperty('constant',real=1.0, imag=0.0)))

ml.save('materials')

Assign materials and define four voltage sources per array. Ensure consistent assignment of positive and negative terminals across all ports.

###first array materials and ports

nsem load material library 'materials.h5'

nsem assign volume substrate material 'FR-4'

nsem assign volume 7 13 19 material 'FR-4'

nsem assign volume {radome} material 'glassfiber'

nsem assign surface {dipole_top} {dipole_bot} material 'PEC'

nsem assign surface 34 35 51 52 68 69 material 'PEC'

nsem assign volume {tower} 28 material 'PEC'

nsem assign surface {GND} material 'PEC'

nsem voltage source 'port_101' pos surface {port_pos} neg surface {port_neg} impedance 50

nsem voltage source 'port_102' pos surface 32 neg surface 33 impedance 50

nsem voltage source 'port_103' pos surface 49 neg surface 50 impedance 50

nsem voltage source 'port_104' pos surface 66 neg surface 67 impedance 50

###second array materials and ports

nsem assign volume 29 35 40 45 material 'FR-4'

nsem assign volume 50 material 'glassfiber'

nsem assign surface 227 226 243 244 259 260 275 276 material 'PEC'

nsem assign surface 228 material 'PEC'

nsem voltage source 'port_201' pos surface 224 neg surface 225 impedance 50

nsem voltage source 'port_202' pos surface 241 neg surface 242 impedance 50

nsem voltage source 'port_203' pos surface 257 neg surface 258 impedance 50

nsem voltage source 'port_204' pos surface 273 neg surface 274 impedance 50

Meshing

Repeat the meshing on the second array like the first one. 

###meshing

surface all scheme pave

#{mesh=0.3/1*1000/10}

###first array meshing

#port meshing

group 'feed1' add surface {port_pos} {port_neg} 32 33 49 50 66 67

curve common_to surface in feed1 interval 1

mesh surface in feed1

#antenna meshing

surface {dipole_top} {dipole_bot} 34 35 51 52 68 69 size {mesh/4}

mesh surface {dipole_top} {dipole_bot} 34 35 51 52 68 69

surface 14 16 17 18 size {mesh/4}

mesh surface 14 16 17 18

surface {GND} size {mesh/1.5}

mesh surface {GND}

surface not is_meshed in volume 1 7 13 19 size {mesh/4}

mesh surface not is_meshed in volume 1 7 13 19

#radome meshing

surface not is_meshed in volume {radome} size {mesh}

mesh surface not is_meshed in volume {radome}

###second array meshing

group 'feed2' add surface 224 225 241 242 257 258 273 274

curve common_to surface in feed2 interval 1

mesh surface in feed2

#antenna meshing

surface 227 226 243 244 259 260 275 276 size {mesh/4}

mesh surface 227 226 243 244 259 260 275 276

surface 228 size {mesh/1.5}

mesh surface 228

surface not is_meshed in volume 29 35 40 45 size {mesh/4}

mesh surface not is_meshed in volume 29 35 40 45

#radome meshing

surface not is_meshed in volume 50 size {mesh}

mesh surface not is_meshed in volume 50

### telecom tower meshing

surface not is_meshed in volume {tower} size {mesh}

mesh surface not is_meshed in volume {tower}

surface not is_meshed in volume 28 size {mesh}

mesh surface not is_meshed in volume 28

block 1 surface all

quality surface all shape global draw mesh

save cub5 "two_arrays.cub5" overwrite journal

Fig. 2 Model with the mesh quality plotted.

Simulation Setup

Create a simulation.py file to configure the simulation parameters. Since the structure is electrically large, use the compression solver, which performs matrix compression and leverages near- and far-field coupling to efficiently represent the system.

from nsem import *

import numpy as np

config = 'two_arrays'

model = Configuration(f'{config}_sim') #configure simulation name

model.set_cub5_filename(f'{config}.cub5') #load the mesh file

model.set_order(1) #set basis order, default is 1

model.set_model_scale(0.001) #convertion to mm

model.set_frequencies(freq_beg=0.5, freq_end=1.5) #set frequency sweep from 0.5 to 1.5 GHz

model.set_solve_type(solver='COMPRESS') #change the solver type

model.save()

report = Report(f'{config}_report', f'{config}_sim') #create a report object

report.set_frequencies(np.linspace(0.5, 1.5, 11))

step = 2 #set the step for theta and phi angles 

theta_scan = np.linspace(0, 180, int(180/step+1)) #theta angles from 0 to 180 degrees

phi_scan = np.linspace(0, 360, int(360/step)) #phi angles from 0 to 360 degrees

report.request_far_fields_grid(theta_scan, phi_scan) #request far-field data

report.save() #save the report configuration

model.run() #run the simulation

report.run() #run the report generation

Post-Processing

Create postprocessing.py to extract simulation data and visualize results. In this example, three scenarios are evaluated:

1. Both arrays scanned to boresight 

2. Both arrays scanned 10-deg down 

3. One array scanned 10-deg up, one array scanned 10-deg down

import numpy as np

import matplotlib.pyplot as plt

from nsem.postprocessing import *

#simulation data

config = 'two_arrays'

post = PostProcess(f'{config}_sim')

freq = np.asarray(post.get_frequencies())  

s = post.get_s_parameters(freq_evaluate=freq)  

S21 = s[4:8, 0:4, :]   #array1 to array2

S12 = s[0:4, 4:8, :]   #array2 to array1

#phase / weights for each array

def progressive_weights(N, phase_deg_per_elem=0.0):

    k = np.deg2rad(phase_deg_per_elem)

    w = np.exp(1j * k * np.arange(N))

    return w.astype(complex)

Set up 0 phase shifts on both arrays in order to study case #1.

#phase progressions for the two arrays

w1 = progressive_weights(4, phase_deg_per_elem=0.0)    #array1

w2 = progressive_weights(4, phase_deg_per_elem=0.0)    #array2

#coupling vs frequency

C21 = np.einsum('i,ijk,j->k', np.conj(w2), S21, w1)   #array1 to array2

C12 = np.einsum('i,ijk,j->k', np.conj(w1), S12, w2)   #array2 to array1

# Convert to dB

coupling21_dB = 20 * np.log10(np.abs(C21))

coupling12_dB = 20 * np.log10(np.abs(C12))

#weights for all 8 ports to calculate gain and patterns

w_gain = np.zeros(8, dtype=complex)

w_gain[0:4] = w1       #array1 ports on

w_gain[4:8] = w2      #array2 ports on

post_gain = PostProcess(f'{config}_report')  # create a post-processing object for the report

freq_gain = post_gain.get_frequencies()

theta = post_gain.get_obs_theta()

phi = post_gain.get_obs_phi()

gain = post_gain.get_gain('spherical',weights=w_gain)  #get gain with specified amplitude/phase distribution

theta_idx,_ = post_gain.get_nearest(theta, 0.0)

phi0_idx,_  = post_gain.get_nearest(phi, 0.0)

phi90_idx,_  = post_gain.get_nearest(phi, 90.0)

theta90_idx,_ = post_gain.get_nearest(theta, 90.0)

theta0_idx,_ = post_gain.get_nearest(theta, 0.0)

freq_idx,_ = post_gain.get_nearest(freq_gain, 1.0)

gain_0 = gain[phi0_idx, theta90_idx, 0, freq_idx, 1]

print(f"Boresight gain (dBi): {gain_0:.2f}")

gain_max = np.squeeze(gain[phi0_idx, theta90_idx, 0, :, 1])

gain_copol_phi0  = gain[phi0_idx, :, 0, freq_idx,1]

gain_copol_phi90 = gain[phi90_idx, :, 0, freq_idx, 0]

gain_xpol_phi0   = gain[phi0_idx, :, 0, freq_idx, 0]

gain_xpol_phi90  = gain[phi90_idx, :, 0, freq_idx, 1]  

gain_copol_theta90 = gain[:, theta90_idx, 0, freq_idx, 1]   

gain_copol_theta0  = gain[:, theta0_idx, 0, freq_idx, 1]

gain_xpol_theta90  = gain[:, theta90_idx, 0, freq_idx, 0]

#Plots

fig = plt.figure(figsize=(12, 10))

gs = fig.add_gridspec(2, 2, height_ratios=[1, 1])

ax1 = fig.add_subplot(gs[0, :])                

ax2 = fig.add_subplot(gs[1, 0])                 

ax3 = fig.add_subplot(gs[1, 1], projection='polar')  

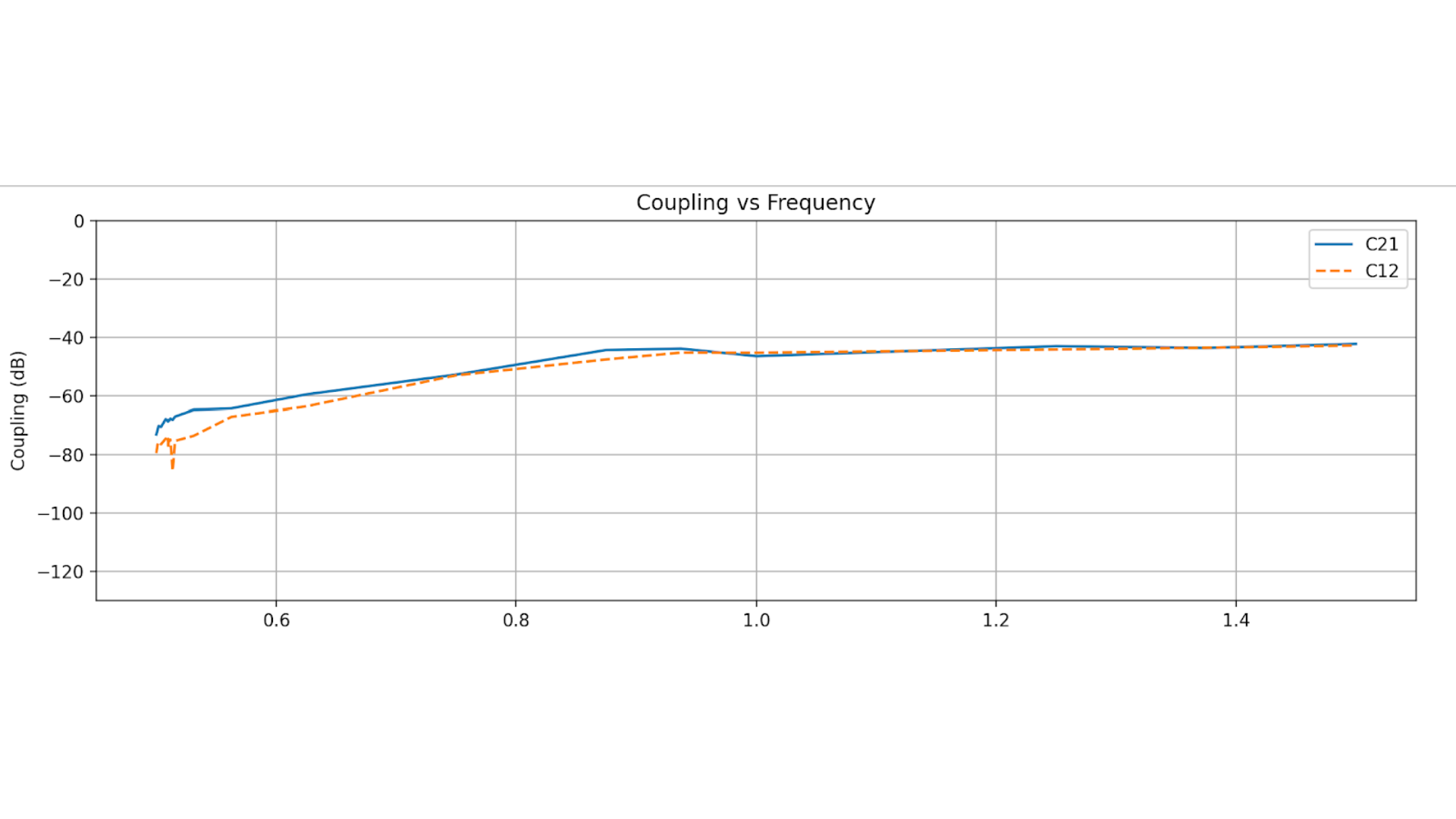
#Coupling vs frequency

ax1.plot(freq, coupling21_dB, label='C21')

ax1.plot(freq, coupling12_dB, '--', label='C12')

ax1.set_ylim(-130, 0)

ax1.set_xlabel('Frequency (GHz)')

ax1.set_ylabel('Coupling (dB)')

ax1.set_title('Coupling vs Frequency')

ax1.grid(True)

ax1.legend()

Fig. 3 Coupling between arrays for the 1st case.

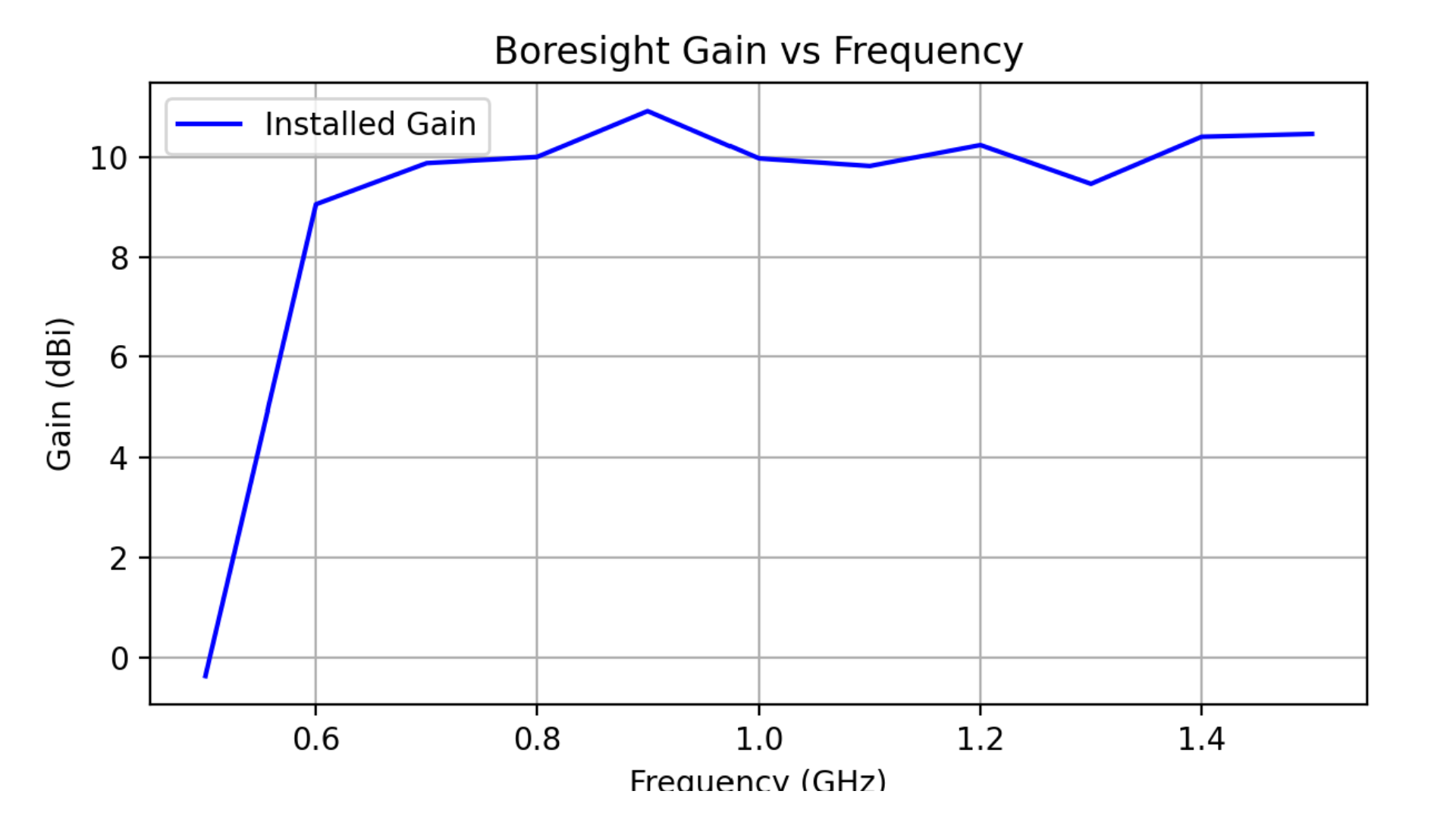
# gain vs frequency

ax2.plot(freq_gain, gain_max, label='Installed Gain', color='blue')

ax2.set_xlabel('Frequency (GHz)')

ax2.set_ylabel('Gain (dBi)')

ax2.set_title('Boresight Gain vs Frequency')

ax2.grid(True)

ax2.legend()

Fig. 4 Boresight gain over frequency for one array

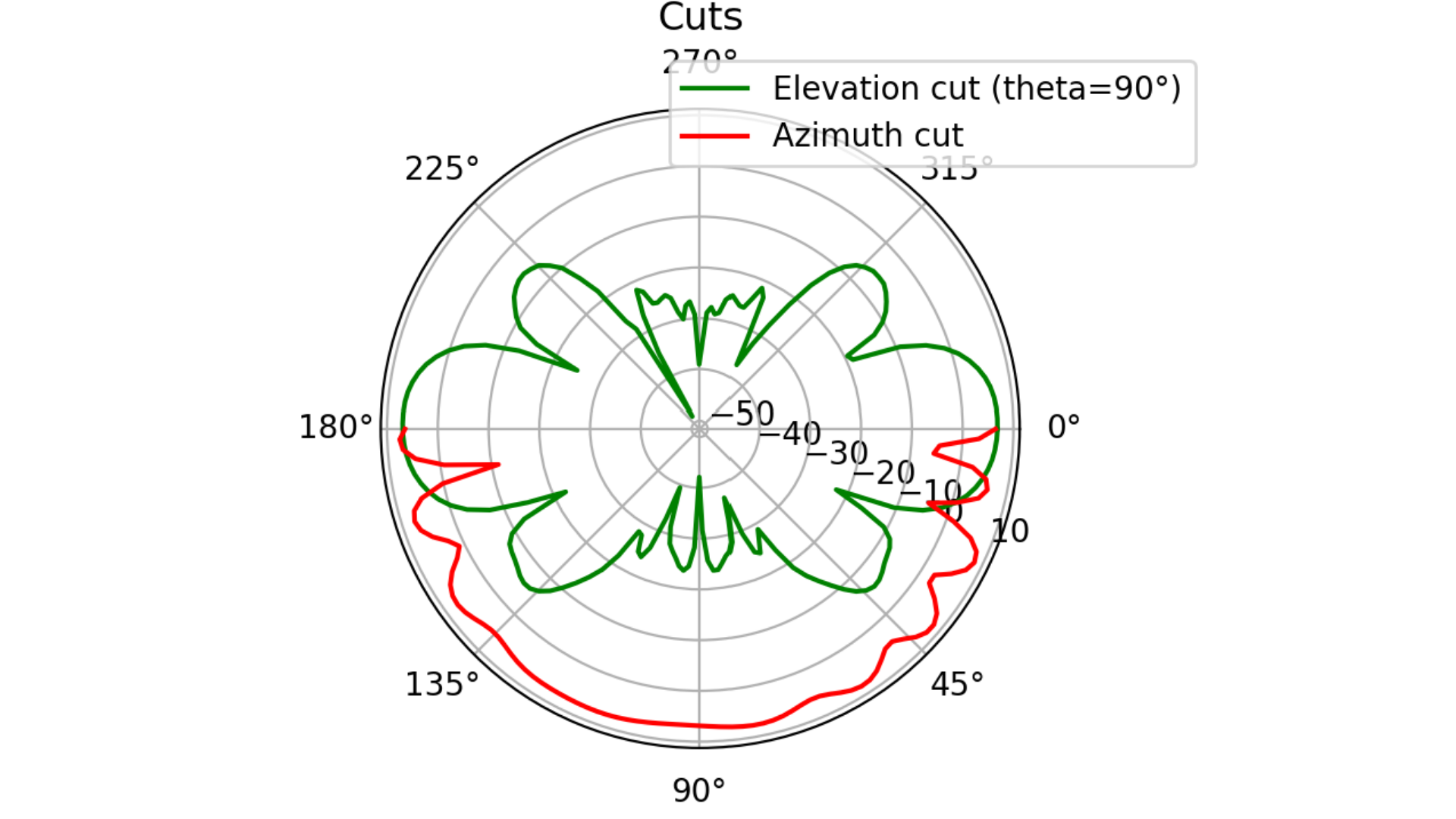
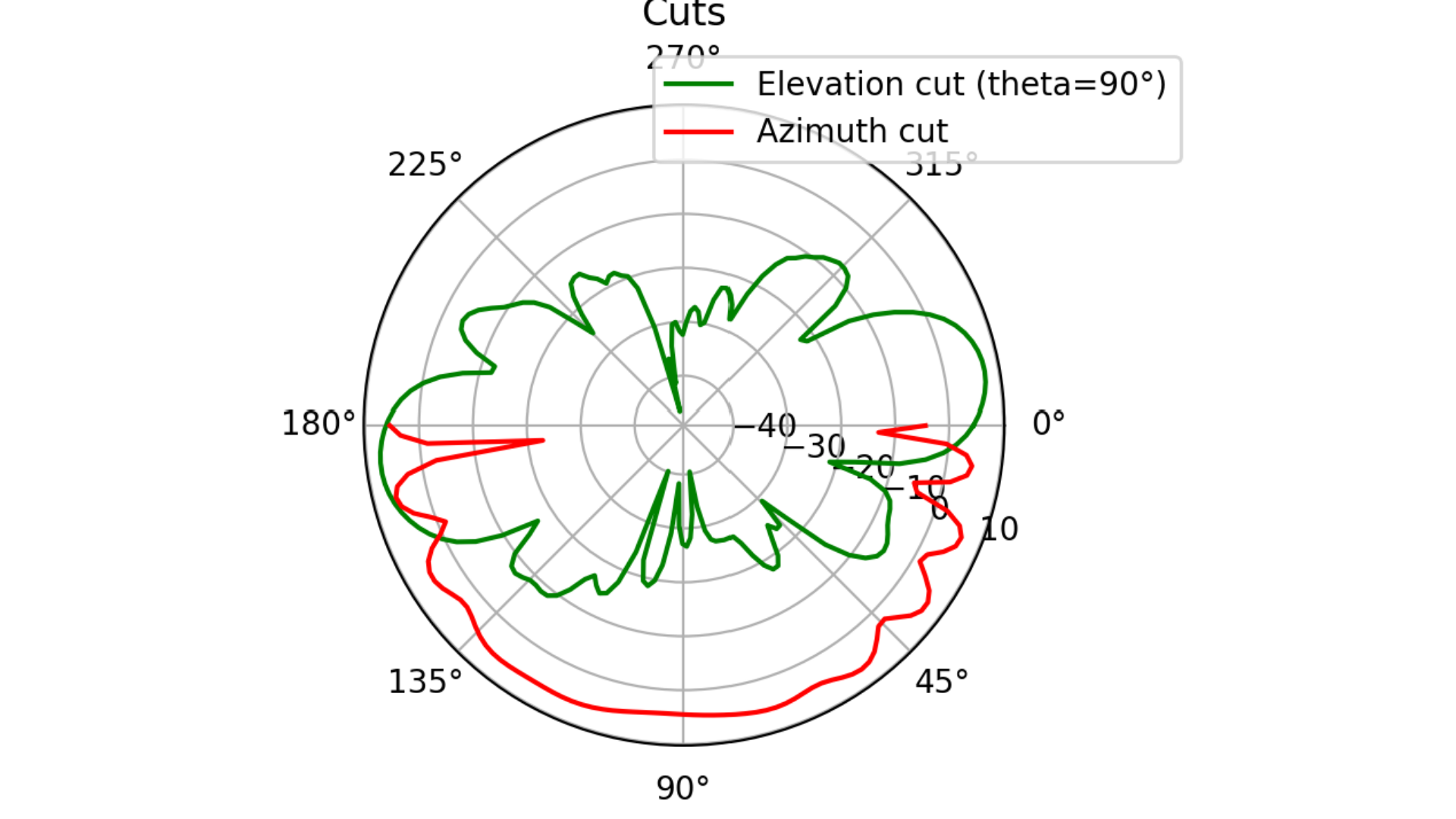
# Polar cut

ax3.plot(np.deg2rad(phi), gain_copol_theta90, color='green', label='Elevation cut (theta=90°)')

ax3.plot(np.deg2rad(theta), gain_copol_phi0, label=f'Azimuth cut', color='red')

ax3.set_title('Cuts') 

ax3.set_theta_direction(-1)        

ax3.grid(True)

ax3.legend(loc='upper right', bbox_to_anchor=(1.3, 1.1))

plt.tight_layout()

Fig. 5 Elevation and Azimuth cuts: 1st case.

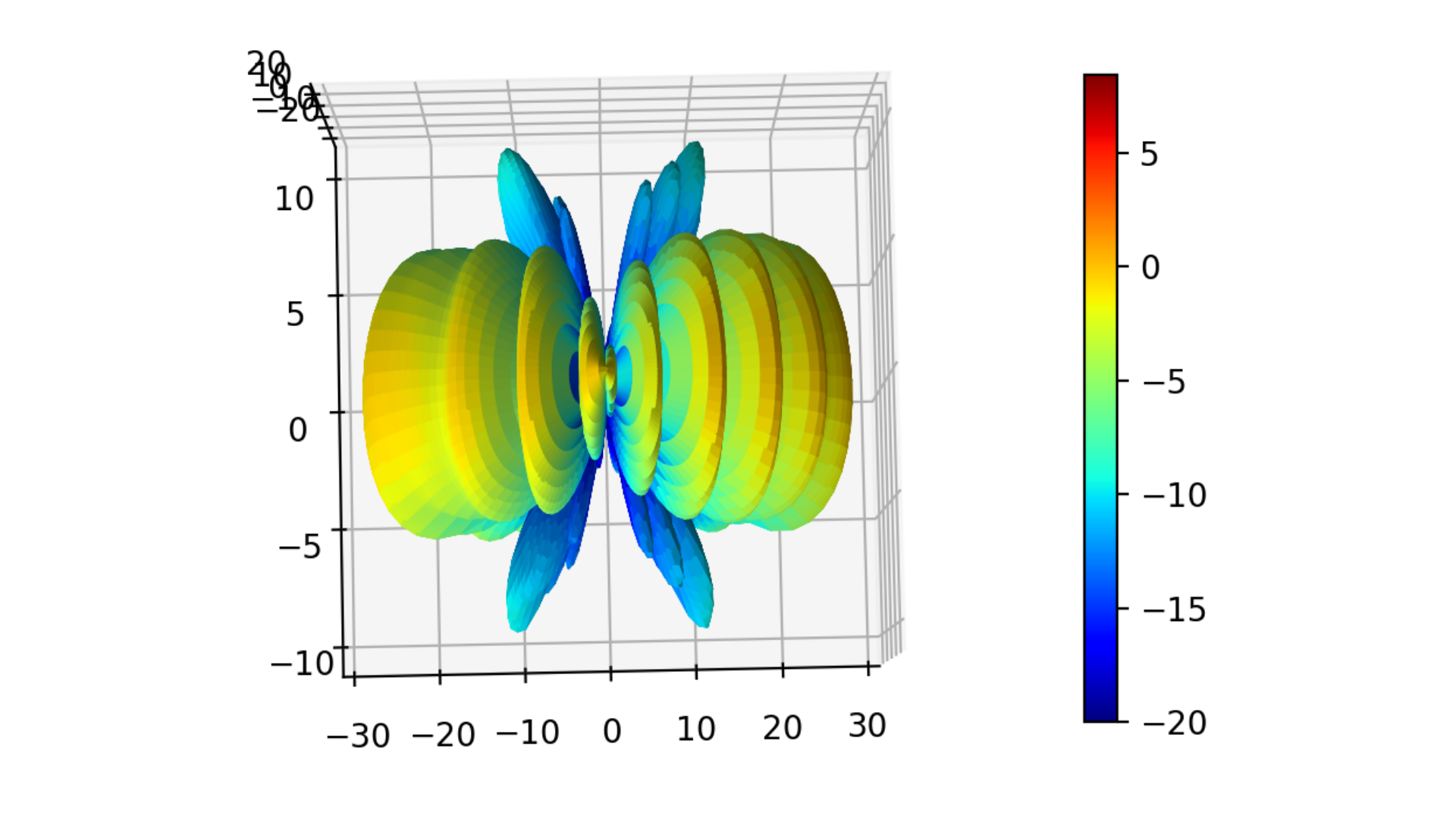
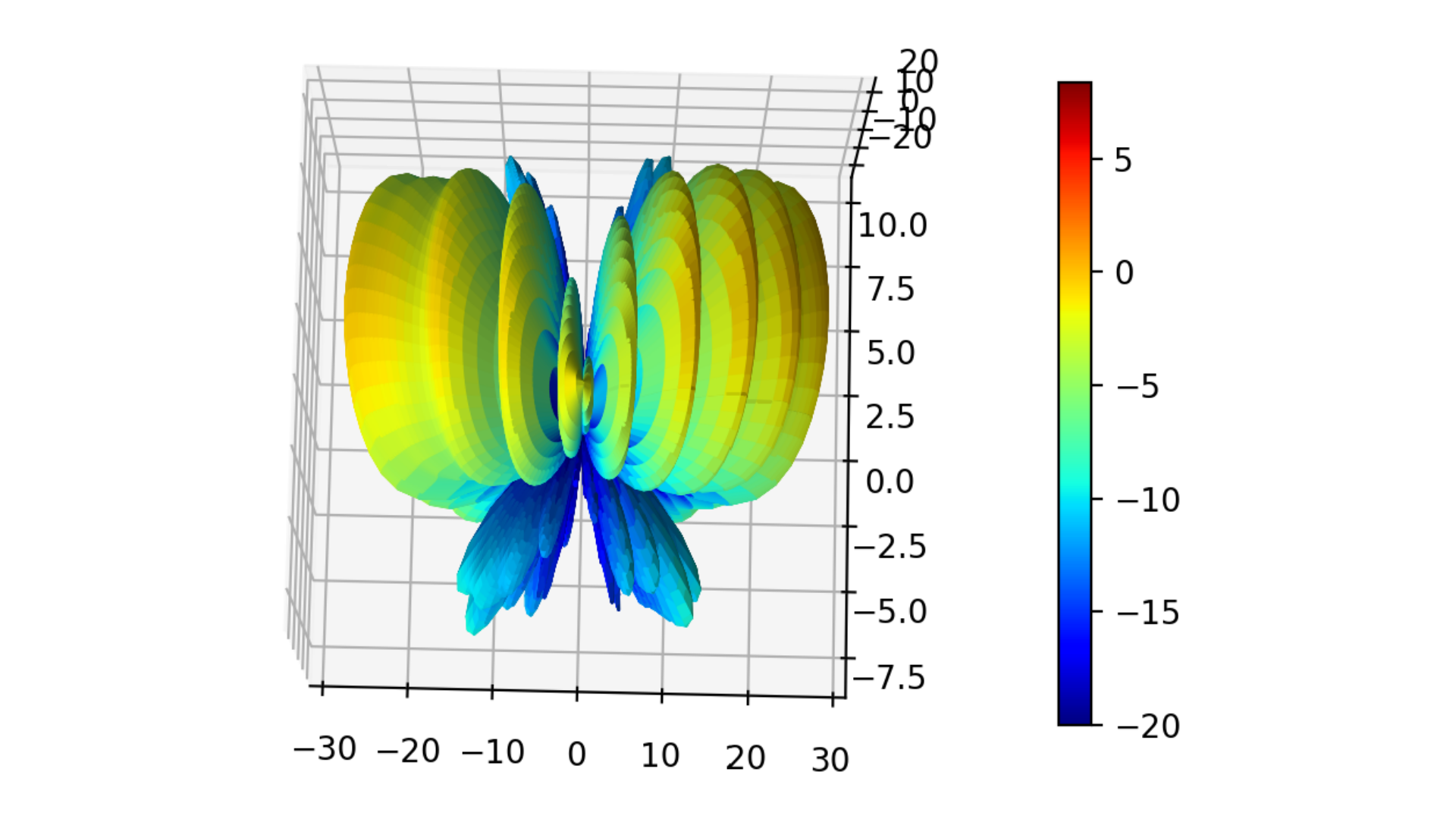
fig3d,ax3d = post_gain.plotPolar3D(gain[:,:,0,freq_idx,1], -20.0,20.0)

fig3d.show()

plt.show()

Fig. 6 3D gain pattern: 1st case.

Change phase shifts on both arrays in order to study case #2. 

#phase progressions for the two arrays

w1 = progressive_weights(4, phase_deg_per_elem=-30.0)    #array1

w2 = progressive_weights(4, phase_deg_per_elem=-30.0)    #array2

Fig. 7 Elevation and Azimuth cuts: 2nd case.

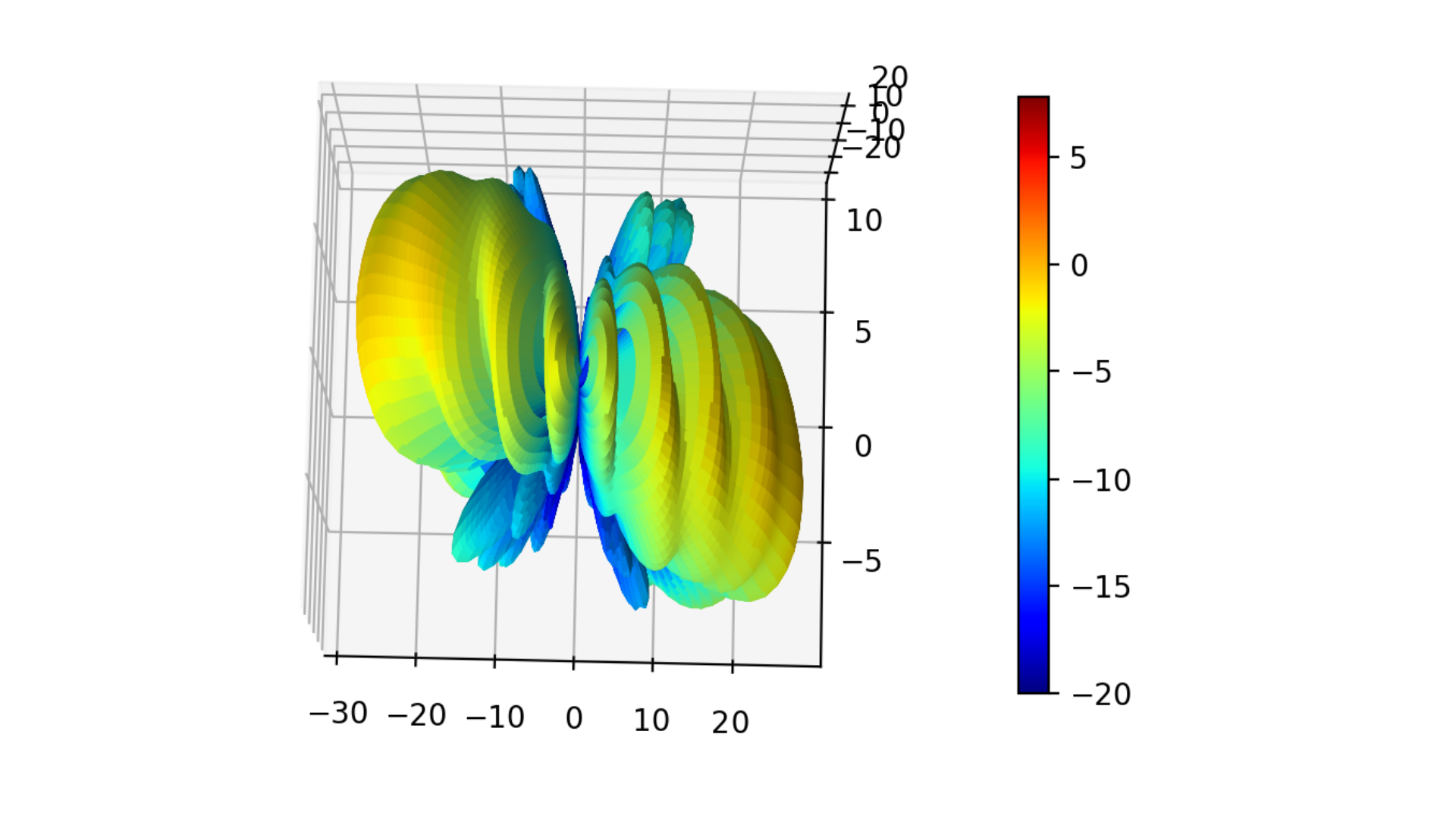
Fig. 8 3D gain pattern: 2nd case.

Change phase shifts on one of the arrays in order to study case #3. 

#phase progressions for the two arrays

w1 = progressive_weights(4, phase_deg_per_elem=-30.0)    #array1

w2 = progressive_weights(4, phase_deg_per_elem=30.0)    #array2

Fig. 9. Coupling between arrays for the 3rd case.

Fig. 10 Elevation and Azimuth cuts: 3rd case.

Fig. 11 3D gain pattern: 3rd case.